喜提最劣解（常数最大解）。第一遍甚至读错题一个小时，喜提视力最好奖。

不难发现题目要求除了给定的黑点外其他点不能染成黑色（就是读错在这里了）。

因此不难发现，若一个灰点周围有至少一个黑点，则这个点要满足两个条件之一。

一：这个点初始染成白色

二：这个点与一个初始染成白色的点相连。

然后就是很基础的东西了，因为相连在树上有儿子和父亲的关系，所以要分讨几种情况。

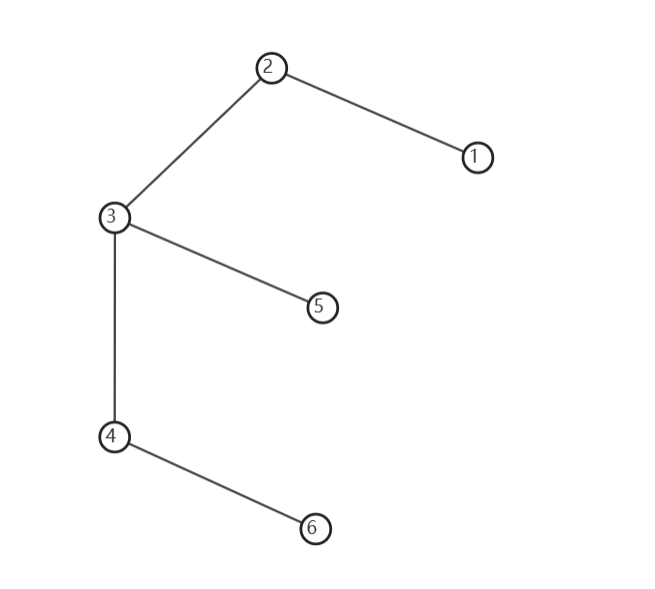
假如说将 $1,5,6$ 染成黑色，答案为 $1$，将 $3$ 染成白色即可，可以手玩一下，就知道怎么设置状态了。

设 $dp_{x,0/1/2/3}$ 分别表示 $x$ 不染成白色/染成白色/不染成白色，但保证父亲染成白色/不染成白色，但保证有至少一个儿子染成白色。

若 $x$ 是 $y$ 的父亲：需要保证 $dp_{y,2}$ 只能通过 $dp_{x,1}$ 转移。

对于至少一个儿子染成白色，先不强制限制，最后加上 $\min(dp_{y,1}-\min(dp_{y,0},dp_{y,1},dp_{y,3}))$ 做一个类似反悔的操作即可。

若 $x$ 初始染成黑色，则所有转移结束后令 $dp_{x,1}\gets \infty$，若 $x$ 周围至少有一个黑点，则所有转移结束后令 $dp_{x,0}\gets \infty$，防止传上去不合法的状态。

最后的答案是 $\min(dp_{1,0},dp_{1,1},dp_{1,3})$。时间复杂度为 $O(n)$。

官方题解。来源：清华大学学生算法协会仓库

出题人：abruce

做法：考虑不能出现新的黑点，那么每个与黑点相邻的点要么它自己一开始染白，要么与其相邻的灰点，即其父亲或儿子一开始被染白。

考虑如下 dp：$f_{u,0},f_{u,1},f_{u,2},f_{u,3}$ 分别表示在 $u$ 染白点，$u$ 儿子染白点，$u$ 留给父亲染白点，$u$ 什么也没干。转移考虑 $u$ 的每种情况和 $u$ 的儿子的每种情况是否适配即可。